Az ötös szorzótábla az, amit mindenki a legkönnyebben meg tud tanulni, hiszen csak 5-re és 0-ra végződnek a szorzatok. Igen ám, de akinek ez is problémát jelent, az hiába mondja sorba a számokat, időt veszít vele, míg eljut mondjuk a 8x5-höz.
Mikor az ötös szorzótáblát tanítottam, a táblai magyarázat közben beugrott egy ötlet, hogy az ujjaink segítségével hogy lehet a korábban magyarázott sorba számolás helyett hamarabb meglátni a végeredményt. Felírtam a táblára az ötös szorzótáblát, majd észrevétettem a tanulókkal, hogy a páros számoknál a szorzás eredménye nullára végződik, tehát az egyesek helyén mindig 0 van, a tízesek helyén álló szám pedig éppen a fele a szorzandó számának. Ha mondjuk 2-t szorzok öttel, akkor a 2 fele, 1, tehát a szorzat 10, azaz 1 tízes. Ha 4-gyel szorzok, 4-nek a fele 2, az eredmény tehát 20, azaz 2 tízes.
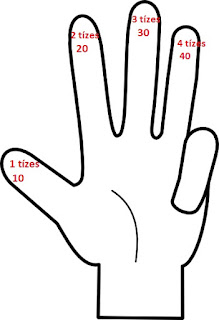
Ezt az ujjainkon is tudjuk mutatni:
Keresem például a 8 és az 5 szorzatát. 8 ujjat mutatok, mondom a szorzást, és közben bezárom az ujjaim felét, és az eredmény 4 nyitva maradt ujj, de ez már tízesekkel számolva negyvenet jelent.
 |
| 8 x 5= |
A páratlan számoknál megfigyeltük, hogy a szorzás eredménye mindig 5-re végződik. Megbeszéltük, hogy páratlan számot nem tudunk felezni, ezért az ujjainkon páros számot mutatunk, de tudjuk, hogy a bezárt ujjainkhoz adni kell még ötöt.
Vagyis ha mondjuk a 7 x 5 eredményére vagyunk kíváncsiak, 6-ot mutatunk, bezárjuk a felét, megkapjuk a 30-at, hozzáadunk még ötöt, és megkapjuk, hogy a szorzat 35.
Nekünk bevált, remélem másnak is hasznos lesz!


Nincsenek megjegyzések:
Megjegyzés küldése